Exemplo De Valor Absoluto E Valor Relativo – O conceito de Valor Absoluto e Valor Relativo é fundamental em matemática, fornecendo uma base para compreender e resolver diversos problemas em áreas como física, engenharia, finanças e economia.
Este artigo explorará a definição, propriedades e aplicações dos valores absolutos e relativos, oferecendo uma visão abrangente desses conceitos.
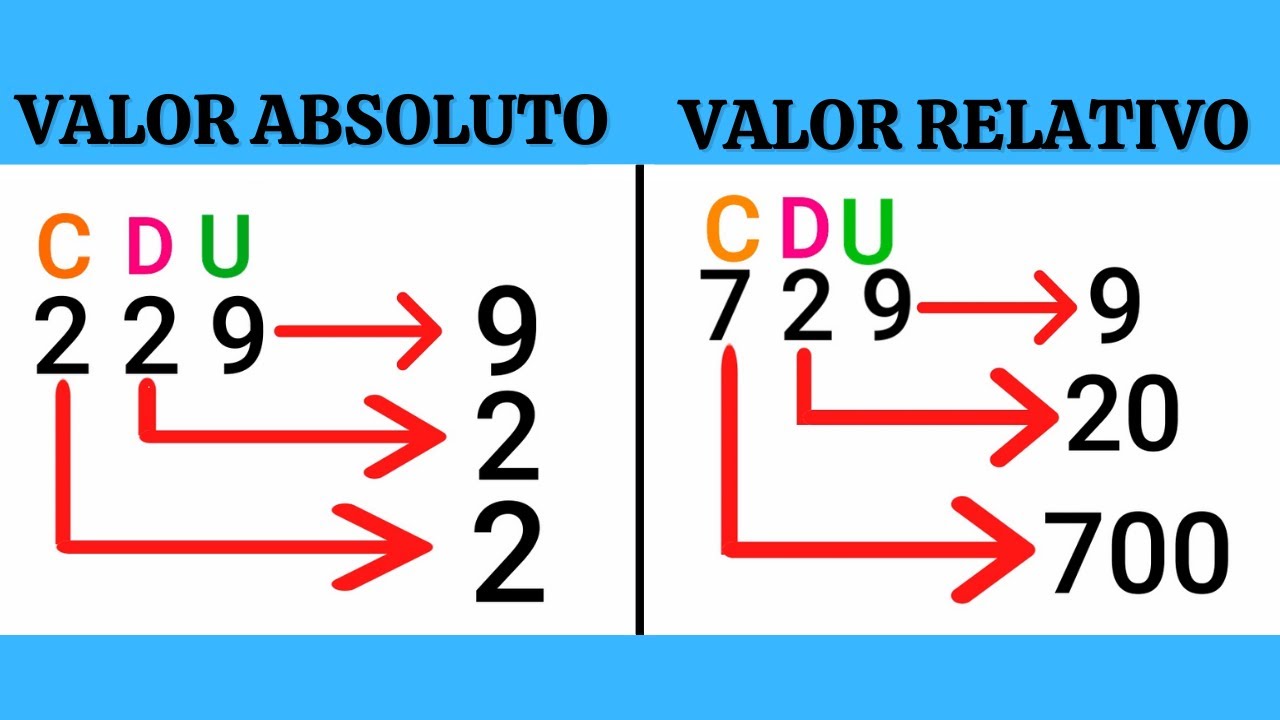
Conceito de Valor Absoluto e Valor Relativo
Introdução
Em matemática, os conceitos de valor absoluto e valor relativo são ferramentas essenciais para medir e comparar números. O valor absoluto representa a distância de um número em relação a zero na reta numérica, enquanto o valor relativo indica o sinal (positivo ou negativo) do número.
Valor Absoluto, Exemplo De Valor Absoluto E Valor Relativo
O valor absoluto de um número real x, denotado por |x|, é definido como:
|x| = x, se x ≥ 0-x, se x< 0
A Segunda Lei de Newton, também conhecida como Lei da Aceleração, afirma que a aceleração de um objeto é diretamente proporcional à força líquida que atua sobre ele e inversamente proporcional à sua massa. Exemplos cotidianos dessa lei podem ser observados em diversas situações, como o movimento de um carro acelerando ( 2 Lei De Newton Exemplos Do Dia A Dia ), a queda de um objeto devido à gravidade ou a desaceleração de um ciclista ao frear.
Por exemplo, o valor absoluto de 5 é 5, e o valor absoluto de -5 também é 5. Isso ocorre porque a distância de 5 e -5 em relação a zero é a mesma.
Valor Relativo
O valor relativo de um número real x é simplesmente o próprio número x. Ele indica se o número é positivo ou negativo.
Números positivos têm valor relativo positivo, enquanto números negativos têm valor relativo negativo. Por exemplo, o valor relativo de 5 é positivo, enquanto o valor relativo de -5 é negativo.
Importância do Valor Absoluto
O valor absoluto tem várias aplicações importantes em matemática, incluindo:
- Medir a distância entre dois números na reta numérica
- Resolver equações e desigualdades envolvendo valores absolutos
- Definir funções com valores absolutos, como a função valor absoluto f(x) = |x|
Aplicações do Valor Absoluto

O valor absoluto possui diversas aplicações em diferentes áreas do conhecimento.
A Segunda Lei de Newton, que afirma que a força resultante sobre um objeto é igual à massa do objeto multiplicada pela sua aceleração, pode ser observada em vários aspectos do nosso cotidiano. Por exemplo, ao empurrar um carrinho de compras, a força aplicada pelo indivíduo é igual à massa do carrinho multiplicada pela sua aceleração, conforme descrito em 2 Lei De Newton Exemplos Do Dia A Dia .
Na física e na engenharia, o valor absoluto é usado para calcular grandezas como velocidade, distância e força. Por exemplo, se um carro viaja a 60 km/h, o valor absoluto de sua velocidade é 60 km/h, independentemente da direção em que está se movendo.
Finanças e Economia
Em finanças e economia, o valor absoluto é usado para medir o ganho ou a perda em investimentos. Por exemplo, se um investidor compra uma ação por R$ 10 e a vende por R$ 15, seu ganho é de R$ 5. O valor absoluto desse ganho é de R$ 5, independentemente se o investidor comprou ou vendeu a ação.
Propriedades do Valor Absoluto

O valor absoluto possui diversas propriedades que são fundamentais para simplificar expressões matemáticas. Essas propriedades são listadas abaixo:
Propriedade 1: Não Negatividade
O valor absoluto de qualquer número real é sempre não negativo. Ou seja, |x| ≥ 0 para todo x ∈ R.
Propriedade 2: Igualdade a Zero
O valor absoluto de um número real é zero se e somente se o número for zero. Ou seja, |x| = 0 se e somente se x = 0.
Propriedade 3: Simetria
O valor absoluto de um número real é igual ao valor absoluto do seu oposto. Ou seja, |x| = |-x| para todo x ∈ R.
Propriedade 4: Propriedade Triangular
O valor absoluto da diferença entre dois números reais é menor ou igual à soma dos valores absolutos desses números. Ou seja, |x – y| ≤ |x| + |y| para todos x, y ∈ R.
Propriedade 5: Multiplicação
O valor absoluto do produto de dois números reais é igual ao produto dos valores absolutos desses números. Ou seja, |xy| = |x| |y| para todos x, y ∈ R.
Propriedade 6: Divisão
O valor absoluto do quociente de dois números reais é igual ao quociente dos valores absolutos desses números, desde que o denominador não seja zero. Ou seja, |x/y| = |x| / |y| para todos x, y ∈ R, y ≠ 0.
Essas propriedades podem ser usadas para simplificar expressões matemáticas, como:
- |x + y| ≤ |x| + |y|
- |x – y| ≥ ||x| – |y||
- |x/y| = |x| / |y|, para y ≠ 0
Representações Gráficas do Valor Absoluto: Exemplo De Valor Absoluto E Valor Relativo

O gráfico do valor absoluto de uma função pode ser usado para entender as propriedades da função. O gráfico do valor absoluto é uma função em forma de V que é simétrica em relação ao eixo y. O valor absoluto de um número é sempre positivo, então o gráfico do valor absoluto está sempre acima do eixo x.
O gráfico do valor absoluto pode ser usado para encontrar os valores máximo e mínimo de uma função. O valor máximo é o ponto mais alto do gráfico e o valor mínimo é o ponto mais baixo do gráfico. O gráfico do valor absoluto também pode ser usado para encontrar os zeros de uma função.
Os zeros de uma função são os pontos onde o gráfico cruza o eixo x.
Comparação do Gráfico do Valor Absoluto com o Gráfico de Outras Funções
O gráfico do valor absoluto é diferente do gráfico de outras funções, como a função quadrática. O gráfico de uma função quadrática é uma parábola que se abre para cima ou para baixo. O gráfico do valor absoluto é uma função em forma de V que é simétrica em relação ao eixo y.
O gráfico do valor absoluto também é diferente do gráfico de uma função linear. O gráfico de uma função linear é uma linha reta. O gráfico do valor absoluto é uma função em forma de V que é simétrica em relação ao eixo y.
Em resumo, os valores absolutos e relativos são ferramentas matemáticas essenciais que permitem quantificar grandezas e estabelecer relacionamentos entre elas. Sua compreensão é crucial para resolver problemas em vários campos, fornecendo uma base sólida para análises e tomadas de decisão.

.gallery-container {
display: flex;
flex-wrap: wrap;
gap: 10px;
justify-content: center;
}
.gallery-item {
flex: 0 1 calc(33.33% – 10px); /* Fleksibilitas untuk setiap item galeri */
overflow: hidden; /* Pastikan gambar tidak melebihi batas kotak */
position: relative;
margin-bottom: 20px; /* Margin bawah untuk deskripsi */
}
.gallery-item img {
width: 100%;
height: 200px;
object-fit: cover; /* Gambar akan menutupi area sepenuhnya */
object-position: center; /* Pusatkan gambar */
}
.image-description {
text-align: center; /* Rata tengah deskripsi */
}
@media (max-width: 768px) {
.gallery-item {
flex: 1 1 100%; /* Full width di layar lebih kecil dari 768px */
}
}

